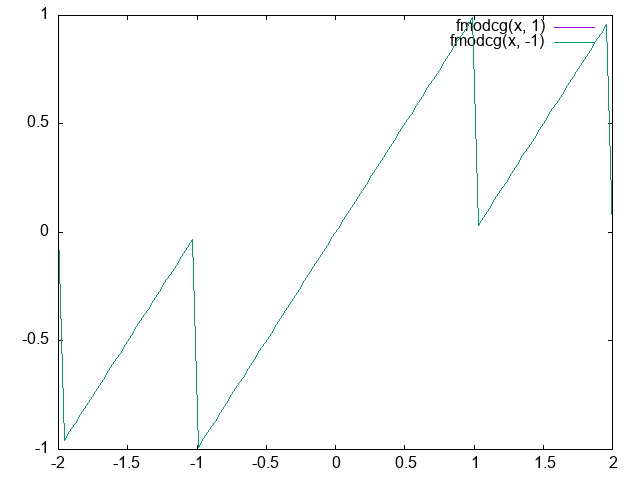TL;DR
シェーダー言語によってその言語組み込みの fmod() (mod()) の実装は異なるため注意する必要がある.
挙動の罠に引っかからないためには自前で実装するのが安全である.
GLSL
// Equivalent to mod() in GLSL.
float fmodglsl(float x, float y)
{
return x - y * floor(x / y);
}
HLSL
// Equivalent to fmod() in HLSL.
float fmodhlsl(float x, float y)
{
return x - y * trunc(x / y);
}
CG, Unityのshaderlab(CGPROGRAM, HLSLPROGRAM かに依存しない)
// Equivalent to fmod() in CG.
float fmodcg(float x, float y)
{
const float c = frac(abs(x / y)) * abs(y);
return x < 0 ? -c : c;
}
fmodについて
fmod() とは浮動小数点の剰余の計算を行う関数である.
シェーダー特有のものではなく,C言語の <math.h> にも存在しているような普遍的な計算である.
Unityのshaderlabでの確認方法
僕個人としてはshaderlabをいじることがほとんどである.
そのため,shaderlabでの組み込み関数 fmod() の実装がどうなっているかを調べることにした.
実装を見るためには,組み込み関数の fmod() と自前で用意した剰余関数から生成される命令(Direct X11用)を比較するのが手っ取り早い.
とりあえず,以下のコードで確認することにした.
FmodImpl.shader
Shader "koturn/FmodImpl"
{
Properties
{
_MainTex ("Main texture", 2D) = "white" {}
_Color ("Multiplicative color for _MainTex", Color) = (1.0, 1.0, 1.0, 1.0)
_Value01 ("Value01", Float) = 23.0
_Value02 ("Value02", Float) = 3.7
[KeywordEnum(Operator, Native Func, CG, HLSL, GLSL)]
_ModType ("Mod operation type", Float) = 2 // Default: Back
[Enum(UnityEngine.Rendering.CullMode)]
_Cull ("Cull", Float) = 2 // Default: Back
[Enum(UnityEngine.Rendering.CompareFunction)]
_ZTest ("ZTest", Float) = 4 // Default: LEqual
[Enum(Off, 0, On, 1)]
_ZWrite ("ZWrite", Float) = 0 // Default: Off
[Enum(UnityEngine.Rendering.BlendMode)]
_SrcFactor ("Src Factor", Float) = 5 // Default: SrcAlpha
[Enum(UnityEngine.Rendering.BlendMode)]
_DstFactor ("Dst Factor", Float) = 10 // Default: OneMinusSrcAlpha
}
SubShader
{
Tags
{
"RenderType" = "Transparent"
"Queue" = "Transparent"
}
Cull [_Cull]
ZWrite [_ZWrite]
ZTest [_ZTest]
Blend [_SrcFactor] [_DstFactor]
Pass
{
CGPROGRAM
#pragma target 3.0
#pragma vertex vert
#pragma fragment frag
#pragma multi_compile_local_fragment _MODTYPE_OPERATOR _MODTYPE_NATIVE_FUNC _MODTYPE_CG _MODTYPE_HLSL _MODTYPE_GLSL
#include "UnityCG.cginc"
UNITY_DECLARE_TEX2D(_MainTex);
uniform float4 _Color;
uniform float _Value01;
uniform float _Value02;
float fmodcg(float x, float y)
{
const float c = frac(abs(x / y)) * abs(y);
return x < 0 ? -c : c;
}
float fmodglsl(float x, float y)
{
return x - y * floor(x / y);
}
float fmodhlsl(float x, float y)
{
return x - y * trunc(x / y);
}
struct appdata
{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
struct v2f
{
float4 vertex : SV_POSITION;
float2 uv : TEXCOORD0;
};
v2f vert(appdata v)
{
v2f o;
o.vertex = UnityObjectToClipPos(v.vertex);
o.uv = v.uv;
return o;
}
fixed4 frag(v2f i) : SV_Target
{
float4 col = UNITY_SAMPLE_TEX2D(_MainTex, i.uv) * _Color;
#if defined(_MODTYPE_NATIVE_FUNC)
col.a = fmod(_Value01, _Value02);
#elif defined(_MODTYPE_OPERATOR)
col.a = _Value01 % _Value02;
#elif defined(_MODTYPE_CG)
col.a = fmodcg(_Value01, _Value02);
#elif defined(_MODTYPE_HLSL)
col.a = fmodhlsl(_Value01, _Value02);
#elif defined(_MODTYPE_GLSL)
col.a = fmodglsl(_Value01, _Value02);
#endif
return col;
}
ENDCG
}
}
}
生成コード
部分的に抜粋する.
組み込み関数のfmod
今回の検証対象である. 生成された命令からNVidiaのCgの言語仕様に書かれているのと同様の実装になっていることがわかる.
0: div r0.x, cb0[3].x, cb0[3].y 1: ge r0.y, r0.x, -r0.x 2: frc r0.x, |r0.x| 3: movc r0.x, r0.y, r0.x, -r0.x 4: mul o0.w, r0.x, cb0[3].y
また,CGPROGRAM か HLSLPROGRAM かに依らず同じコードが生成された.
挙動をCgの実装に統一しているのだろう.
演算子
演算子 % を用いた場合でもコンパイルは通るのだが,組み込み関数の fmod() を用いた場合とは異なるコードが生成されていた.
0: mul r0.x, cb0[3].y, cb0[3].x 1: ge r0.x, r0.x, -r0.x 2: movc r0.x, r0.x, cb0[3].y, -cb0[3].y 3: div r0.y, l(1.000000, 1.000000, 1.000000, 1.000000), r0.x 4: mul r0.y, r0.y, cb0[3].x 5: frc r0.y, r0.y 6: mul o0.w, r0.y, r0.x
これをシェーダーコードに翻訳すると下記のようになる.
float fmodop(float x, float y)
{
const float xy = x * y;
const float a = (xy >= -xy) ? y : -y;
const float b = frac((1.0 / a) * x);
return a * b;
}
計算結果は浮動小数点計算における誤差を無視すれば,組み込み関数の fmod() と一致する.
生成されているコード量としてあまり効率的でないように思われるが実際はどうなのだろうか?
例えば,
3: div r0.y, l(1.000000, 1.000000, 1.000000, 1.000000), r0.x 4: mul r0.y, r0.y, cb0[3].x
は
div r0.y, cb0[3].x, r0.x
でいいのでは?などと思ったりする.

fmodglsl
float fmodglsl(float x, float y)
{
return x - y * floor(x / y);
}
0: div r0.x, cb0[3].x, cb0[3].y 1: round_ni r0.x, r0.x 2: mad o0.w, -cb0[3].y, r0.x, cb0[3].x
floor() は round_ni 命令に対応しており,命令名はおそらくRound to Negative Infinityのことで,負の無限大への丸めを意味するのだろう.
y が正のときは正の値を,y が負のときは負の値を返すようになっている.
x / y が負数のときの挙動が fmodhlsl() と異なり,正負に関係なく周期的な挙動をするため,素直に扱いやすいと思う.

fmodhlsl
float fmodhlsl(float x, float y)
{
return x - y * trunc(x / y);
}
0: div r0.x, cb0[3].x, cb0[3].y 1: round_z r0.x, r0.x 2: mad o0.w, -cb0[3].y, r0.x, cb0[3].x
trunc() は round_z 命令に対応しており,命令名はおそらくRound to Zeroのことで,0への丸めを意味するのだろう.
x / y が負数のときの挙動が fmodglsl() と異なり,正負で周期的な挙動が切り替わる形である.
y の符号が反転したとしても同じ値を返す.

fmodcg
float fmodcg(float x, float y)
{
const float c = frac(abs(x / y)) * abs(y);
return x < 0 ? -c : c;
}
生成される命令としては組み込み関数の fmod() と一致している.
前述の2つよりも命令数が少し多い.
0: div r0.x, cb0[3].x, cb0[3].y 1: frc r0.x, |r0.x| 2: mul r0.x, r0.x, |cb0[3].y| 3: lt r0.y, cb0[3].x, l(0.000000) 4: movc o0.w, r0.y, -r0.x, r0.x
誤差を考慮しなければ算出される値は fmodhlsl() と同じである.
ただし,前述の2つと比較すると,正または負に誤差が発生するので,この関数の返却値に対して積・商を行った結果をそのまま floor() や ceil() に通すと想定外の値となることがある.
(fmodglsl や fmodhlsl を用いた場合と異なる結果になる)
あまりこの実装を用いるメリットはないように思われるが....